Ok so here’s the rules
- I just bet on red every time
- I start with 1 dollar
- every time I lose, I triple my previous bet
- every time I win I restart
I’m going to simulate 10 games
- Game 1 - Bet $1 Lose
- Game 2 - Bet $3 Lose
- Game 3 - Bet $9 Win $18
- Game 4 - Bet $1 Lose
- Game 5 - Bet $3 Lose
- Game 6 - Bet $9 Win $18
- Game 7 - Bet $1 Lose
- Game 8 - Bet $3 Lose
- Game 9 - Bet $9 Lose
- Game 10 - Bet $18 Win $36
In this simulation I’m losing at a rate of 70%. In reality the lose rate is closer to 52%. I put in $54 but I’m walking away with $72, basically leaving the building with $18.
Another example. Let’s pretend I walk in with $100,000 to bet with. I lose my first 10 games and win the 11th.
- 1 lose
- 3 lose
- 9 lose
- 27 lose
- 81 lose
- 243 lose
- 729 lose
- 2187 lose
- 6561 lose
- 19683 lose
- 59049 win $118098
$88573 spent out of pocket, $118098 won
Walk out with roughly $29525.
I get most casinos won’t let you be that high but it’s a pretty extreme example anyway, the likelyhood of losing 10/11 games on 48% odds is really unlikely.
So help me out here, what am I missing?
This is the Martingale system, it will 100% work if you have infinite money and can bet infinite amounts.
It won’t work on any table that has a 0 and/or 00. The reason those green numbers exist is to give the house an edge over high rollers who can sustain a martingale strategy.
It works even with 0 and 00 - but only if you have infinite money and there is no limit to bets. So long as there is finite money, or limited bets you will - statistically - hit a run of losses that exceeds your money.
Maximum bets and the fact that money is limited is what breaks this, once you hit the maximum bet odds are slightly against you winning on that next turn because of the 0 and 00; and so eventually you will lose as you hit running up to the max bet and then lose on that turn.
Lol this is irrelevant
Me: “bets 1 infinity dollars”
Loses
Me: “bets 3 infinities of dollars”
I thought this was a pretty good in-depth explanation of the infinite case and the finite case: https://www.youtube.com/watch?v=zTsRGQj6VT4
You can’t have an infinite amount since past a certain mass it will collapse onto itself and create a black hole. (or other practical limits) So eventually you lose anyway.
It’s been tried before, the House always wins.
https://en.m.wikipedia.org/wiki/Martingale_(betting_system)
Roulette in particular has no skill involved, only various table bets, all of which have a House edge. The only guarantee in Roulette is that if you play long enough, you will lose all of your money. The only thing you are in control of is how much money you bring to the table, and when you stop.
Another way of thinking about it is betting your entire bankroll for 99.9…% certainty that you will win $1.
Say you go into the casino with $1000.
Bet:
$1 lose. $3 lose. $9 lose. $27 lose. $81 lose. $243 lose. $729 oh wait you can't bet that much, you only have $457 left. Dang, do you bet $457 or find another $272? Bet $457 and you win $914! Congrats you're now only down $86! Or maybe you lost and are down $1000. Or maybe you scrounged up $272 so you could keep playing Bet 729 and lose. Now you're down $1272. Or Bet 729 and you win 1458. Pay back the $272 you borrowed from your buddy, you're still up $186. You just bet $729 dollars for a %50 chance of winning $186.But what are the chances of getting 6 or 7 losses in a row? 1 in 64, or 128 respectively, actually worse because roulette wheels aren’t 50/50, they’re 18/19 (18 wins and 19 losses in 37 plays on average) or worse. So losing 6 times in a row will happen 1 in 54 plays, 7 losses is 1 in 106.
Google says roulette wheels spin 55 times per hour so with your strategy you will lose your bank roll in about one hour assuming your starting bet is 0.1% of your bank roll.
I tried the Martingale Strategy in my early 20’s, thinking I had invented a system that would actually beat the house. I was playing $1 roulette, and had a budget of $100. I did manage to win $400ish, and then I lost 12 times in a row. I busted on the 9th loss, and went back to betting $1 just to see how long it would take to win. I would have needed $4096 to stay in the positive, and I would have won $1 on that last bet.
To make things worse, Vegas now have triple 0 roulette tables. Three zeros in a row. In the same place. Do not play Roulette if you want to win. The only bet in a casino isn’t to the casinos favor is on Craps and it’s called ODDS. But to get to able to play it you have to win against 1.41% house edge first. And it is capped about 10x or 5x of original bet.
If you want to have the best odds against a casino that is hard work and not solid strategy. Counting cards can make money but honestly the amount of work it requires - you are better on the stock market or even in crypto.
Do not gamble against the casino.
The only reason to gambe is to have fun and safe risk with money you decided to spend and to never see again.
Haven’t auto shufflers killed counting cards now anyway?
The House will use multiple decks, I think up to 8 but I haven’t gambled for a few years, + the auto shuffler.
They’ll usually deal about 1 decks worth of cards and then pass all cards through the shuffler.
This means that you have to count 8 decks worth of cards, and they reset that before you can really get much of an advantage.
Vegas now have triple 0 roulette tables
Stupid inflation!
So help me out here, what am I missing?
You’re forgetting that not all outcomes are equal. You’re just comparing the probability of winning vs the probability of losing. But when you lose you lose much bigger. If you calculate the expected outcome you will find that it is negative by design. Intuitively, that means that if you do this strategy, the one time you will lose will cost you more than the money you made all the other times where you won.
I’ll give you a short example so that we can calculate the probabilities relatively easily. We make the following assumptions:
- You have $13, which means you can only make 3 bets: $1, $3, $9
- The roulette has a single 0. This is the best case scenario. So there are 37 numbers and only 18 of them are red This gives red a 18/37 to win. The zero is why the math always works out in the casino’s favor
- You will play until you win once or until you lose all your money.
So how do we calculate the expected outcome? These outcomes are mutually exclusive, so if we can define the (expected gain * probability) of each one, we can sum them together. So let’s see what the outcomes are:
- You win on the first bet. Gain: $1. Probability: 18/37.
- You win on the second bet. Gain: $2. Probability: 19/37 * 18/37 (lose once, then win once).
- You win on the third bet. Gain: $4. Probability: (19/37) ^ 2 * 18/37 (lose twice, then win once).
- You lose all three bets. Gain: -$13. Probability: (19/37) ^ 3 (lose three times).
So the expected outcome for you is:
$1 * (18/37) + 2 * (19/37 * 18/37) + … = -$0.1328…
So you lose a bit more than $0.13 on average. Notice how the probabilities of winning $1 or $2 are much higher than the probability of losing $13, but the amount you lose is much bigger.
Others have mentioned betting limits as a reason you can’t do this. That’s wrong. There is no winning strategy. The casino always wins given enough bets. Betting limits just keep the short-term losses under control, making the business more predictable.
All your math above is irrelevant and your last paragraph is completely wrong. Table limits are the reason this strategy won’t work…
If you have a large enough bank roll and continuously double your bet after a loss, you can never lose without a table limit.
Source: data analyst.
If you have a large enough bank roll and continuously double your bet after a loss, you can never lose without a table limit.
Unless your bank roll is infinite, you always lose in the average case. My math was just an example to show the point with concrete numbers.
In truth it is trivial to prove that there is no winning strategy in roulette. If a strategy is just a series of bets, then the expected value is the sum of the expected value of the bets. Every bet in roulette has a negative expected value. Therefore, every strategy has a negative expected value as well. I’m not saying anything ground-breaking, you can read a better write-up of this idea in the wikipedia article.
If you don’t think that’s true, you are welcome to show your math which proves a positive expected value. Otherwise, saying I’m “completely wrong” means nothing.
This is just factually incorrect. Losing is always an option, even if you have a billion dollars so you can double your bet ~30 times, you could still lose the weighted coin toss 30 times. On top of that, all the money that’s ever existed still only gets you like 50 spins on the roulette table, exponential growth is a bitch. OPs strategy of tripling their bet only goes for about 13 rounds before OP is slinging around a million dollars. Even if they just won the lottery, round 19 puts them out a cool billion.
Also this strategy is foolish in so many ways because you’re just playing to hopefully break even, and like everything in a casino, the odds of you breaking even before running out of cash ALWAYS favors the house.
Source: Statistics.
Data scientist who does not know that 18/37 means you lose.
Remember, betting red isn’t a 50/50 chance of winning. 0 and 00 are green. So your odds at winning are about 48% with 0, or 47% with 00. Same with odd/even bets. There’s a reason casinos add the 0’s. They aren’t in the business to give you money.
That’s a reason OP went with tripling the bet instead of the more common doubling when people independently discover this system.
Yes but a 45% win chance is the same long term losing plan no matter how much you bet. I could bet 10 times the amount every time I lose and I’ll still have a 45% chance of winning.
Yes that is true… if you end at a “random” point (running out of money for example). But if you can always end at a win (particularly a large one after a string of many losses) then that changes things, the odds become much less relevant because you are manipulating them.*
The problem is that consistently doing so would require genuinely unlimited money and no betting limits, since the number of losses-that-can-happen-in-a-row is itself unlimited. With that little detail the Martingale system would actually work.
Then again if you have unlimited money then why bother to gamble?*(Actually I sorta take back my first comment in this thread, the odds aren’t why to triple, just growing the pot faster each win is)
Thanks for all the responses. Out of curiosity I threw together a quick simulator to try out different variations.
https://roulette-test.netlify.app/
Needless to say, you usually blow everything you came in with:
This is good.
For example, with a million dollar pot and tripling the bet, usually less than 1000 games is safe, you’ll win a small percentage over the initial amount.But sometimes…
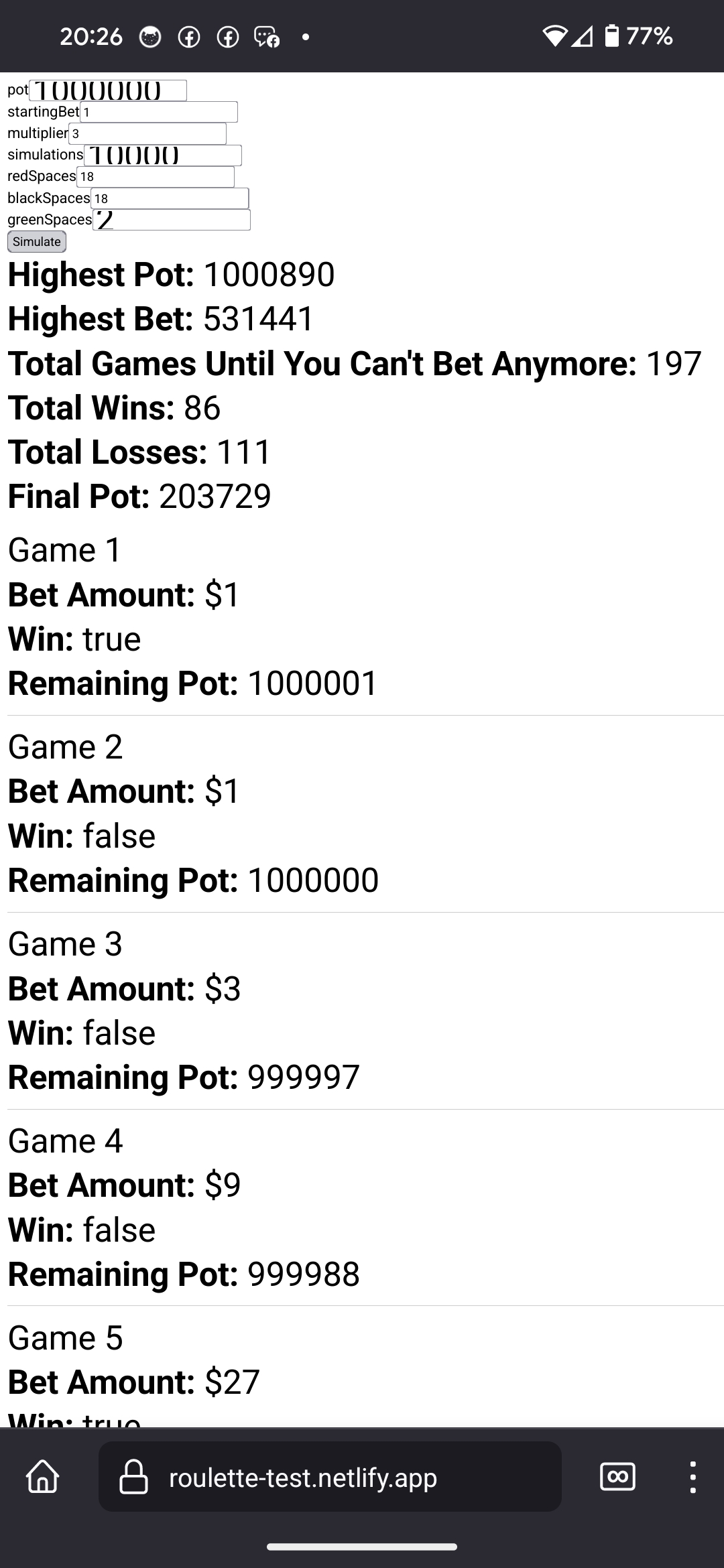
Lol, looks terrible on mobile, just updated it to look nicer
I didn’t get through all the comments, but most of the top ones and haven’t yet seen the most basic casino check to stop these strategies is a table maximum. Same with doubling your bet each hand you lose at black jack, one bad run and you hit table max and you can’t raise your bet far enough
That’s easy though, you just go to higher max table. The hard part is having enough money to sustain the string of losses. And of course the casino sets minimum and max bets at tables, ensuring they don’t align with this strategy.
That last part is key, higher max table comes with a higher minimum bet so the ratio stays roughly the same. I suppose you could move tables as your bet needed to increase and switch back to the low table if you manage to win one making cash reserves the main limiting factor, but I’ve always envisioned the table rules are set in a way to prevent someone with deep pockets from exploiting strategies
What if I bet on black?
Expanding a bit more on what everyone else says: This strategy works, as long as you never lose n times in a row, where n is the number of bets it takes to bet ALL of the money you currently have.
So the more money you bring with you, the longer you can make this strategy work - but the more devastating it’ll be once you inevitably lose.
If you go with a doubling strategy instead of a tripling strategy, that means you have to lose floor(log₂(x+1)) times to realize an unrecoverable loss (you don’t have enough to make your next bet), or one more than that to lose absolutely everything. With your tripling strategy the calculation is floor(log₃(2*x+1)). x is the amount of money you had after the last “reset”.
So if you go to the casino with $100,000, your strategy will work as long as you don’t lose 11 times in a row - once you do, you’ve suffered your devastating unrecoverable loss. Every time your money triples you can last one more loss. Tripling your money is very difficult with this strategy, as most of the time when you win, it’s a small amount relative to what you’re holding - you need large losing streaks to make a real difference, and large losing streaks make reaching the threshold of an unrecoverable loss easier, obviously.
Others have said it already, but - you can use this to win in the short term if you have a lot of money and only want to win a little bit more. If you use this strategy in the long term you will lose everything.
The fundamental theorem of gambling is a mathematically proven fact which states that as long as the house has an edge, there is no betting strategy that has a positive long-term expected value.
The limiting factor is called “Gambler’s ruin”.
With the first rise of online casinos (pre 2010), a friend of mine thought he had rigged the system by more or less the same strategy. I think the usual approach is actually to double the bet.
Well…in the end he won a debt of several 10k€ before he had to quit. This put a huge strain on his early adulthood.
Congratulations, you’ve invented the Martingale betting system and are well on your way to becoming an adept probability theorist
The short answer is that casinos account for this by changing the profit returns and the odds of making a profit at all so that catastrophic losses are much more likely
Betting limits.
Also, n^3 grows fast.
It’s 3^n, not n^3. n^3 is actually way slower.
You’re missing the house edge that means over time they’ll effectively always win. Gambling is a suckers game.
This is what is known in the betting industry as “chasing your losses” and is a warning sign of a problem gambler who requires an intervention.






